Now, we’ll introduce selection into the equation, which will violate
condition #2 for Hardy-Weinberg equilibrium. If a population is not in
equilibrium, the allele frequencies will change from generation to generation.
In the case of the peppered moth, we’ll assume that none of the light
color moths survive. Therefore, in our next generation we’ll have
the Aa genotype, and the AA genotype,
but none of the aa genotype. In our example
of a thousand offspring, that leaves us with 640 AA and
320 Aa. What happens in the next generation,
after these remaining moths breed randomly?
Due to selection against the aa genotype, we’ve gone from allele a frequency of 0.2 to 0.167 in one generation.
Now, let’s assume the surviving genotypes AA and Aa reproduce, leading to 1000 individuals in the next (second) generation. Based on what we’ve just calculated, in the second generation, the proportion of:
AA is 0.689 X 1000 = 689
Aa is 0.282 X 1000 = 282
aa is 0.289 X 1000 = 29
Assuming none of the aa genotype moths survive to reproduction, the population will now consist of 689 AA and 282 Aa (total = 971) individuals. The proportion of A alleles in the mating population, p’, will be:
(689 + 689 + 282)/1942 = 0.855
The proportion of a alleles in the mating population, q’, will be:
1 – 0.855 = 0.145
In two generations, we’ve gone from allele a frequency of 0.2 to 0.167 and to 0.145, when selection against aa genotype is present.
In the illustration below, with selection for the A allele, its frequency will increase and approach 1.0, while the frequency of the a allele will approach 0 and eventually be lost.
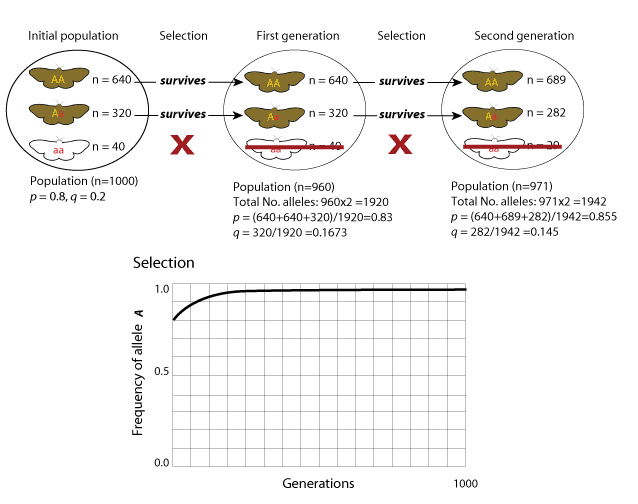
The frequency of the a allele will continue to decline as long as the same selection is applied each subsequent generation. It is interesting to note that removing all individuals with the aa genotype from each parental generation does not remove the aa genotype completely from the population, because aa can arise from crossing the heterozygotes, Aa and Aa. Without removing the heterozygotes (which do not show the a allele phenotypically), it will take a long time for the a allele to disappear completely from the population.
Let’s test your knowledge of this topic:
A population of 100 diploid individuals originally experiencing Hardy-Weinberg equilibrium consists of 49 AA, 42 Aa and 9 aa individuals. Let’s assume an extreme scenario: A new disease targets and kills only those individuals who are homozygous recessive, aa, so all individuals with the aa genotype do not survive. What is the frequency of the allele A after this selection?
Frequency of A = ____________
Click here for an explanation:
The initial frequency of allele A is (49 + 49 +42)/200 = 0.70.
After selection, only 49 AA and 42 Aa individuals survive, for a total of 91 individuals surviving.
The frequency of allele A, p, is now (49 + 49 + 42)/(91 + 91) = 140/182 = 0.769.
Continuing on the same question, what will the frequency of allele A be if this generation of the population reproduces by random mating? You may assume 100 offspring were produced in the next generation.
Frequency of A = ______________
Click here for an explanation:
After selection, we’ve calculated the frequency of allele A, p, to be 0.77, meaning the frequency of allele a, q, is 1 – 0.769 = 0.231.
The 49 AA and 42 Aa individuals mate randomly to produce the following genotypes in the next generation: (0.77A + 0.23a)2 = 0.591 (AA) + 0.355 (Aa) + 0.053 (aa).
This translates into 59 AA, 36 Aa and 5 aa individuals, where the 5 aa die.
The new frequency of allele A, p’, is (59 + 59 + 36)/(95 + 95) = 154/190 = 0.811.
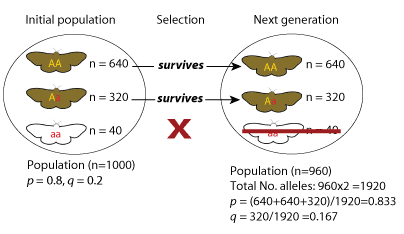 There are now a total of 1920 alleles in the mating population. The proportion of the A alleles in the mating population
will be: (640 + 640 + 320) / 1920 = 0.83 and the proportion of a alleles
will be: 1 – 0.83 = 0.17. You can also calculate the proportion of a alleles by the following: 320/1920 = 0.17. Hence, p is now 0.83 and q is 0.17.
There are now a total of 1920 alleles in the mating population. The proportion of the A alleles in the mating population
will be: (640 + 640 + 320) / 1920 = 0.83 and the proportion of a alleles
will be: 1 – 0.83 = 0.17. You can also calculate the proportion of a alleles by the following: 320/1920 = 0.17. Hence, p is now 0.83 and q is 0.17.