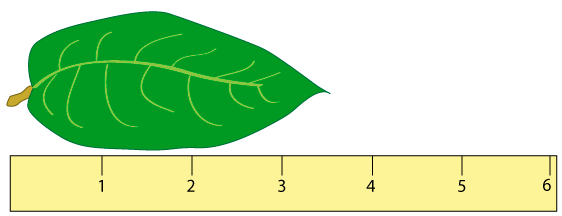
Measuring values
When discussing mathematical measurements in science, it is important to understand that the way a measurement is taken affects its accuracy. For example, you could measure the length of a leaf with a ruler that had markings every centimeter (cm). In this example, illustrated below, the leaf is longer than 3 cm and shorter than 4 cm, so you might estimate that the leaf is 3.5 cm long.

On the other hand, if you measured the same leaf with a ruler that had markings every millimeter (mm), as drawn below, you can see that the end of the leaf actually falls between the markings for 3.5 and 3.6 cm (or 35 and 36 mm). Because it’s closer to the 3.5 marking, you might estimate that the leaf is 3.52 cm (or 35.2 mm) long.
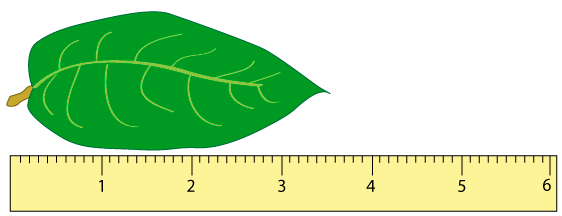
Using the second ruler, it’s possible to estimate that the leaf is 3.52cm long, but it is not possible to measure that accurately with the first ruler. In this way, the number of digits in the measured value gives us an idea of the maximum accuracy of the measurement. These are called significant digits or significant figures.
If you were to make your own measurements, your significant digits should include all of the measurable digits (the digits that correspond to the marks on the ruler) as well as one estimated position beyond the smallest measureable digit (the 5 in 3.5 cm, and the 2 in 3.52 cm). Likewise, if you read that someone else has found a leaf that measures 4.568 cm, you can assume that this person measured with a ruler that had markings every hundredth of a cm and estimated the final digit (the 8 in 4.568).
In some instances, you might only be able to measure a value to the nearest hundred or thousand – or even a larger number! In this case, zeros are used as placeholders for significant digits. For example, in the example used above, the leaf is 35.2 mm long. It is also 35200 micrometers (mm) long – but even if we use mm to discuss the measurement, there are still only three significant figures, since the last non-zero number indicates the first estimated, or uncertain position. Likewise, we could discuss the length of the leaf in meters: the leaf is 0.0352 m long. In this case as well, there are still only three significant figures: the zero is a placeholder.
It is important to note that trailing zeros to the left of a decimal point, but to the right of the first non-zero figure (like the bolded red zeros in 78000) are always considered insignificant. However, because insignificant zeros can be dropped after the decimal point, trailing zeros to the right of the decimal point (like the bolded red zeros in 5.000) are always considered significant.
Calculated values
Some values – like averages or totals – are not measured directly. Rather, they are calculated from measured values. Examples of calculated measurements might be the sum, average, or difference of several measurements. These calculated measurements will only be as good as the least accurate measurement used for calculation. In this case, the calculated values must also follow the rules of significant figures, and the number of significant figures in the calculated value is dependent on the values used in calculation.
A summary of rules used in calculations follows:
For addition and subtraction, it is not the number of significant digits that is important but the “smallest” place of the least precise number being added. For example, if you are measuring the distance you’ve traveled in one day, and you drive 556.1 km (as measured by your car’s odometer) and walk 1.642 km (as measured by a pedometer), it wouldn’t make much sense to assert that you traveled 557.742 km, since you wouldn’t have enough information about how far you had driven your car. To illustrate this, the equation is drawn below, with digits that we are certain of in black, and digits we are uncertain of in red. (Remember that the first uncertain digit is the last significant figure. Zeros are used as uncertain placeholders.) Uncertainty in a digit used in calculation will “contaminate” digits in our answer with uncertainty, so uncertain digits in our answer are also colored red.
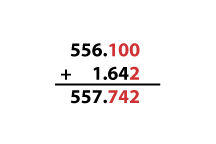
Because our answer, using significant figures, can only include the first uncertain digit, our calculated value is 557.7 km.
For multiplication and division, the calculated value should have the same number of significant digits as the value with the least number of significant digits that is used in calculation. The reason why is illustrated below, once again using black for certain digits and red for uncertain digits:
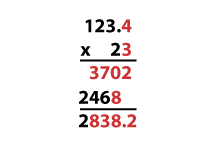
Because only the first uncertain digit is included, our calculated value is 2800, with two significant digits, just like the value 23 used in calculation.
Rounding
When doing calculations using significant figures, you will find it necessary to round your answer to the nearest significant digit. There are therefore a few rules of rounding that help retain as much accuracy as possible in the final answer.
1. Complete all sequential calculations BEFORE doing any rounding, since rounding early reduces the number of significant figures available for subsequent calculations.
2. If the last significant digit is followed by a 6, 7, 8, or 9, round up. Example: 5.677, rounded to three significant digits, is 5.68
3. If the last significant digit is followed by a 0, 1, 2, 3, or 4, simply drop the trailing digits. Example: 561200, rounded to three significant digits, is 561000
4. If the last significant digit is EVEN, and is followed by a 5, drop the trailing digits. Example: 45850, rounded to three significant digits, is 45800
5. If the last significant digit is ODD, and is followed by a 5, round up. Example: 3.47588, rounded to three significant digits, is 3.48
Ambiguous zeros
So what happens if your calculation or measurement ends in a zero? For example, what if you measured a branch that was 200 cm (not 199 or 201 cm) long? The zeros in a measured value of 200 cm in this case appear ambiguous, since it could suggest that there is only one significant digit.
One way to reduce this ambiguity is to use significant figures with scientific notation, which is discussed in the next section.